Clohessy-Wiltshire方程的系统推导

Clohessy-Wiltshire 方程最初由 William H. Clohessy 和 Richard S. Wiltshire 于 1960 年建立。该方程的提出是为了简化复杂的轨道交会问题，这对于涉及多航天器的太空任务至关重要。CW方程为两艘航天器之间的相对运动提供了线性化的近似解，这使得人们能够更精确地设计和执行交会机动。

由于航天器均在中心天体的引力场中运动，其相对运动表现出与地面环境显著不同的非直观特性。本文系统地推导描述该相对运动的动力学方程，从惯性空间中的二体问题出发，通过坐标变换将运动方程在以目标为原点的LVLH旋转坐标系中表示，并最终通过线性化处理，得到通用的Hill’s Equations及其在近圆轨道下的特例——CW Equation

建立动力学模型

惯性系下的绝对运动

在以中心天体质心为原点的地心惯性坐标系中，假设Target与追踪航天器Chaser的运动分别遵循二体问题动力学：

$\ddot{\mathbf{r}}_t + \frac{\mu}{r_t^3}\mathbf{r}_t = \mathbf{0}$ $\ddot{\mathbf{r}}_c + \frac{\mu}{r_c^3}\mathbf{r}_c = \mathbf{a}_c$

其中：

$\mathbf{r}_t$ 和 $\mathbf{r}_c$ 分别是目标和追踪航天器的惯性位置矢量。
$\mu$ 是中心天体的引力常数。
$\mathbf{a}_c$ 是作用在追踪航天器上的单位质量控制力及其他非中心引力扰动。

旋转坐标系下的相对运动

为研究相对运动，建立一个固连在目标航天器上的LVLH坐标系 $O_{xyz}$：

原点 $O$: 目标航天器质心
$Oy$ 轴: 沿 $\mathbf{r}_t$ 方向，即径向
$Oz$ 轴: 沿轨道角动量方向 $\mathbf{h} = \mathbf{r}_t \times \dot{\mathbf{r}}_t$，即法向/跨轨向 Cross-track
$Ox$ 轴: 与 $Oy$ 和 $Oz$ 构成右手坐标系，大致指向轨道速度方向，即切向/沿轨向，aka In-track

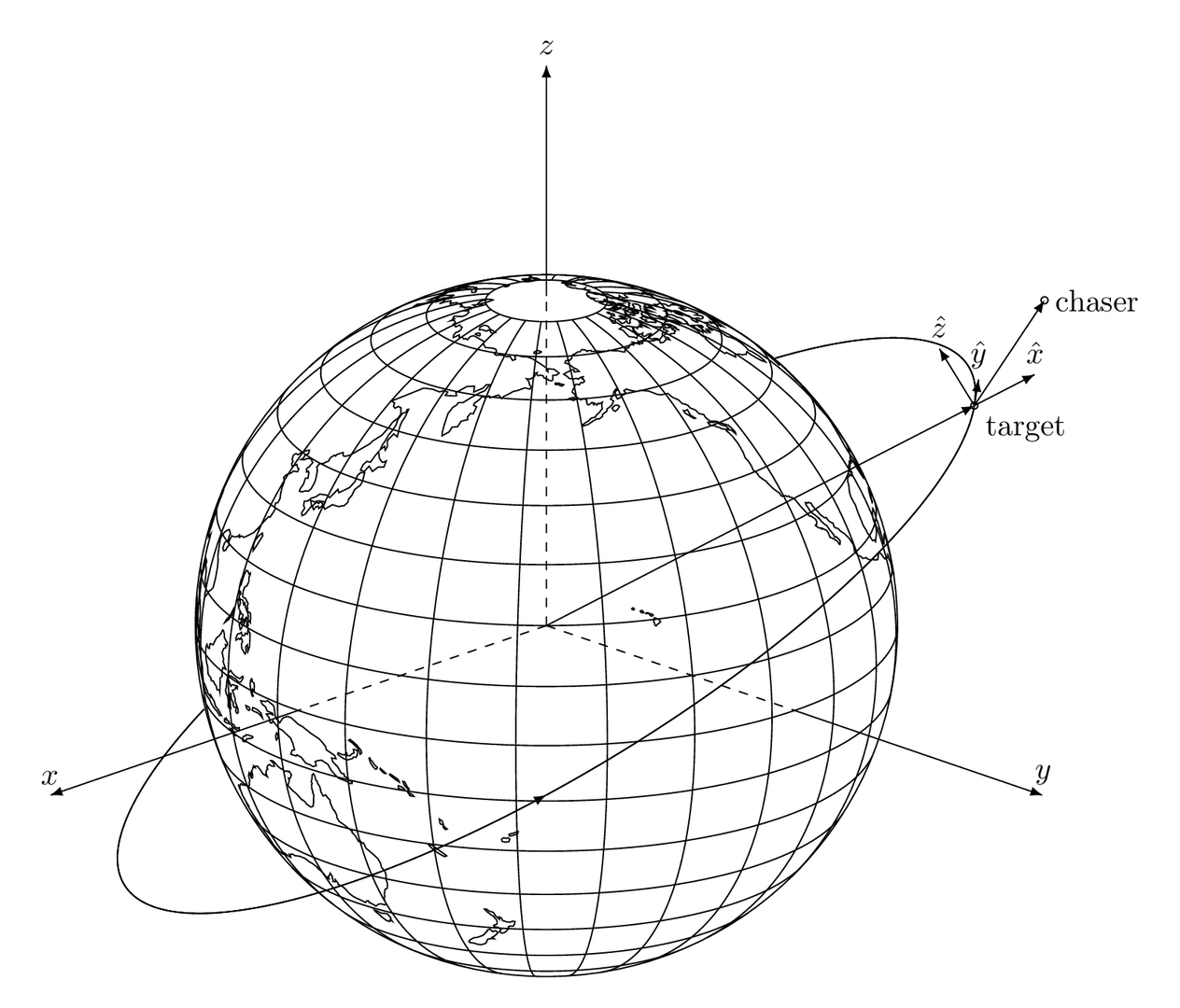
该坐标系以角速度 $\mathbf{\omega}$ 随目标在惯性空间中转动。相对位置矢量定义为 $\mathbf{\rho} = \mathbf{r}_c - \mathbf{r}_t$。根据旋转坐标系下的矢量求导法则，相对加速度 $\ddot{\mathbf{\rho}}$ 可表示为：

$\ddot{\mathbf{\rho}} = \mathring{\mathring{\mathbf{\rho}}} + 2(\mathbf{\omega} \times \mathring{\mathbf{\rho}}) + \dot{\mathbf{\omega}} \times \mathbf{\rho} + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{\rho})$

其中 $\mathring{(\cdot)}$ 表示在LVLH系下对时间的求导。将$\ddot{\mathbf{\rho}} = \ddot{\mathbf{r}}_c - \ddot{\mathbf{r}}_t$代入绝对运动方程，得到：

$\mathring{\mathring{\mathbf{\rho}}} + 2(\mathbf{\omega} \times \mathring{\mathbf{\rho}}) + \dot{\mathbf{\omega}} \times \mathbf{\rho} + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{\rho}) = \frac{\mu}{r_t^3}\mathbf{r}_t - \frac{\mu}{r_c^3}\mathbf{r}_c + \mathbf{a}_c$

该方程是描述相对运动的、精确的非线性动力学方程

左侧为相对运动的运动学项（科里奥利加速度、欧拉加速度、向心加速度），右侧为动力学项（引力差和控制力）

方程线性化

为了获得能够解析分析的线性模型，我们做出以下假设：相对距离远小于轨道半径，即 $||\mathbf{\rho}|| \ll r_t$

引力梯度项的近似

引力差项 $\Delta\mathbf{g} = \frac{\mu}{r_t^3}\mathbf{r}_t - \frac{\mu}{r_c^3}\mathbf{r}_c$ 是方程非线性的主要来源，将其整理为：

$\Delta\mathbf{g} = -\frac{\mu}{r_c^3}\mathbf{\rho} - \left( \frac{\mu}{r_c^3} - \frac{\mu}{r_t^3} \right)\mathbf{r}_t$

由于 $\mathbf{r}_c = \mathbf{r}_t + \mathbf{\rho}$，有 $r_c^2 = \mathbf{r}_c \cdot \mathbf{r}_c = (\mathbf{r}_t + \mathbf{\rho}) \cdot (\mathbf{r}_t + \mathbf{\rho}) = r_t^2 + 2(\mathbf{r}_t \cdot \mathbf{\rho}) + \rho^2$。

在定义的LVLH坐标系中，$\mathbf{\rho}=(x,y,z)^T$ 且 $\mathbf{r}_t = (0, r_t, 0)^T$，则 $\mathbf{r}_t \cdot \mathbf{\rho} = r_t y$。因此：

$r_c^2 = r_t^2 + 2r_t y + \rho^2 = r_t^2 \left( 1 + \frac{2y}{r_t} + \frac{\rho^2}{r_t^2} \right)$

由于 $||\mathbf{\rho}|| \ll r_t$，$\rho^2/r_t^2$ 是二阶小量，可以忽略。

$r_c \approx r_t \left( 1 + \frac{2y}{r_t} \right)^{1/2}$

利用泰勒展开 $(1+\epsilon)^k \approx 1+k\epsilon$，对 $r_c^{-3}$ 进行一阶近似：

$r_c^{-3} = (r_c^2)^{-3/2} \approx [r_t^2(1 + \frac{2y}{r_t})]^{-3/2} = r_t^{-3} \left( 1 + \frac{2y}{r_t} \right)^{-3/2} \approx r_t^{-3} \left( 1 - \frac{3y}{r_t} \right)$

将此近似代回到引力差项的表达式中。

$\Delta\mathbf{g} \approx -\frac{\mu}{r_t^3}\left(1 - \frac{3y}{r_t}\right)\mathbf{r}_c + \frac{\mu}{r_t^3}\mathbf{r}_t$

将 $\mathbf{r}_c = \mathbf{r}_t + \mathbf{\rho}$ 代入:

$\begin{aligned} \Delta\mathbf{g} &\approx -\frac{\mu}{r_t^3}\left(1 - \frac{3y}{r_t}\right)(\mathbf{r}_t + \mathbf{\rho}) + \frac{\mu}{r_t^3}\mathbf{r}_t \\ &= -\frac{\mu}{r_t^3} \left( \mathbf{r}_t + \mathbf{\rho} - \frac{3y}{r_t}\mathbf{r}_t - \frac{3y}{r_t}\mathbf{\rho} \right) + \frac{\mu}{r_t^3}\mathbf{r}_t \\ &= -\frac{\mu}{r_t^3} \left( \mathbf{\rho} - \frac{3y}{r_t}\mathbf{r}_t \right) \quad (\text{忽略二阶小量 } y\mathbf{\rho}) \\ &= -\frac{\mu}{r_t^3}\mathbf{\rho} + \frac{3\mu y}{r_t^4}\mathbf{r}_t \end{aligned}$

将矢量在LVLH坐标系中展开 $\mathbf{\rho}=(x,y,z)^T$ 和 $\mathbf{r}_t = (0, r_t, 0)^T$:

$\begin{aligned} \Delta\mathbf{g} &\approx -\frac{\mu}{r_t^3}(x\mathbf{i} + y\mathbf{j} + z\mathbf{k}) + \frac{3\mu y}{r_t^4}(r_t \mathbf{j}) \\ &= -\frac{\mu}{r_t^3}x\mathbf{i} + \left(-\frac{\mu y}{r_t^3} + \frac{3\mu y}{r_t^3}\right)\mathbf{j} - \frac{\mu}{r_t^3}z\mathbf{k} \\ &= \frac{\mu}{r_t^3}(-x\mathbf{i} + 2y\mathbf{j} - z\mathbf{k}) \end{aligned}$

线性化后的引力差项展示了引力梯度对相对运动的影响

通用 Hill’s Equations

将线性化后的引力项代入精确的非线性动力学方程，并写出其在LVLH坐标系中的分量形式（ $\mathbf{\omega}=(0,0,\omega)^T$），即可得到适用于一般椭圆轨道的通用Hill’s Equations：

$\begin{cases} \ddot{x} - 2\omega\dot{y} - \dot{\omega}y - \omega^2x = -\frac{\mu}{r_t^3}x + a_x \\ \ddot{y} + 2\omega\dot{x} + \dot{\omega}x - \omega^2y = \frac{2\mu}{r_t^3}y + a_y \\ \ddot{z} = -\frac{\mu}{r_t^3}z + a_z \end{cases}$

整理后得到：

$\begin{cases} \ddot{x} - 2\omega\dot{y} - (\omega^2 - \frac{\mu}{r_t^3})x - \dot{\omega}y = a_x \\ \ddot{y} + 2\omega\dot{x} + \dot{\omega}x - (\omega^2 + \frac{2\mu}{r_t^3})y = a_y \\ \ddot{z} + \frac{\mu}{r_t^3}z = a_z \end{cases}$

该方程的系数中含有时变量 $r_t, \omega, \dot{\omega}$，是一个线性时变LTV系统，虽然精确但求解复杂，为了便于求解，进行圆轨道简化

圆轨道简化

圆轨道假设

在实际任务中，目标轨道通常是近圆形的。为了获得一个极简且实用的模型，我们引入理想圆轨道假设。在此条件下，系统参数得到极大简化：

轨道半径 $r_t$ 为常数 $r$。
角速度 $\omega$ 为常数 $n$（平近点角速度），因此角加速度 $\dot{\omega} = 0$。
中心天体引力完全充当向心力，满足 $\omega^2 = n^2 = \mu/r^3$。

C-W方程组

将以上三个条件代入通用Hill’s Equations，即可得到经典的、常系数的Clohessy-Wiltshire Equation：

切向方程:

$\ddot{x} - 2n\dot{y} - (n^2 - \frac{\mu}{r^3})x - 0 = a_x \implies \ddot{x} - 2n\dot{y} = a_x$

径向方程:

$\ddot{y} + 2n\dot{x} + 0 - (n^2 + \frac{2\mu}{r^3})y = a_y \implies \ddot{y} + 2n\dot{x} - 3n^2y = a_y$

法向方程:

$\ddot{z} + \frac{\mu}{r^3}z = a_z \implies \ddot{z} + n^2z = a_z$

最终的C-W方程组为：

$\begin{cases} \ddot{x} - 2n\dot{y} = a_x \\ \ddot{y} + 2n\dot{x} - 3n^2y = a_y \\ \ddot{z} + n^2z = a_z \end{cases}$

物理项分析

C-W方程揭示了近地轨道相对运动的核心物理特性：

科里奥利加速度 ($-2n\dot{y}$ 和 $+2n\dot{x}$): 这是由LVLH旋转坐标系的非惯性效应引起。当追踪器有径向速度$\dot{y}$时，会产生切向的科里奥利加速度；当有切向速度 $\dot{x}$ 时，会产生径向的科里奥利加速度。这是导致轨道运动非直观行为的关键耦合项
引力梯度与离心力组合项 ($-3n^2y$): 这一项源于两个物理效应的叠加。
1. 引力梯度 ($ -2n^2y $): 当追踪器在径向上偏离目标 $y$ 距离时，它受到的地球引力与目标受到的引力不同。这个引力差的线性部分是 $ -2\mu y / r^3 = -2n^2y $。
2. 离心力差异 ($ -n^2y $): 在LVLH系中，追踪器跟随目标以角速度 n 旋转，其位置是 $(x, r+y, z)$。径向上的离心力约为 $n^2(r+y)$，而目标的离心力为 $n^2r$。两者之差的线性部分是 $n^2y$。这两个效应在径向上都起“排斥”作用，总和为 $-3n^2y$。
轨道平面恢复力 (+n^2z): 法向运动是解耦的，表现为一个简单的谐振子。$n^2z$ 项是引力在法向的分量，它始终将偏离轨道平面的航天器拉回平面，形成稳定的振荡。

updated at 2025-08-20

# 轨道动力学 # 多体问题 # GNC