胶片介质的特殊性

胶片通过化学反应记录图像，其记录的信息是连续而非离散的，因此难以直接通过数学方式量化。此外，显影后的胶片图像处理难度较大，无法像数字图像那样方便地进行编辑。这意味着，胶片图像的质量主要依赖胶片本身的性能。

为了客观地测试胶片记录图像的质量，我们主要关注胶片自身的性能指标。以下将介绍一些关键指标，它们不仅有助于全面评价胶片图像质量，还为后续讨论数字图像的质量测试与分析方法奠定基础。

胶片质量的主要指标

锐度

在胶片中，锐度是指在不同密度区域之间再现清晰细节的能力。对于这种能力，往往采用调制传递函数（MTF）来衡量。

MTF的定义

MTF反映了系统在不同空间频率下传递对比度的能力。

通俗地来讲，假设使用胶片记录宽度和间距一致的黑白条纹，如果得到的胶片中黑白条纹的对比度和现实中的完全一样，黑的很黑，白的很白，条纹边界非常清晰，那么其MTF值就为100；但假如得到的胶片中黑白条纹完全混叠在一起，变成一片灰色，完全失去了对比度，那么其MTF值就为0。如果胶片呈现的黑白条纹对比度有所降低，但条纹边界依然存在，那么其MTF值介于0和1之间。

此时通过改变黑白条纹的宽度和间距，就可以理解为在改变胶片记录对象的空间频率，也就可以得到胶片系统在不同空间频率下传递对比度的能力。

MTF值越高，意味着胶片能够更好地呈现场景中的细节与对比度；MTF值越低，说明在拍摄细节丰富的场景时，细节和对比度就会丧失得更多。

测量方法

在测量前，先要定义空间频率的概念。空间频率表示在给定距离内一个规则图案重复出现的次数，例如每毫米100个周期。

在测定MTF时，会使用到具有密度和对比度各异的正弦频率图案的测试母版。

将代表不同空间频率、精确划分的黑白图案，接触印像到待评估的胶片上。这种胶片在标准条件下处理，以获得下图中左侧所示的图像。

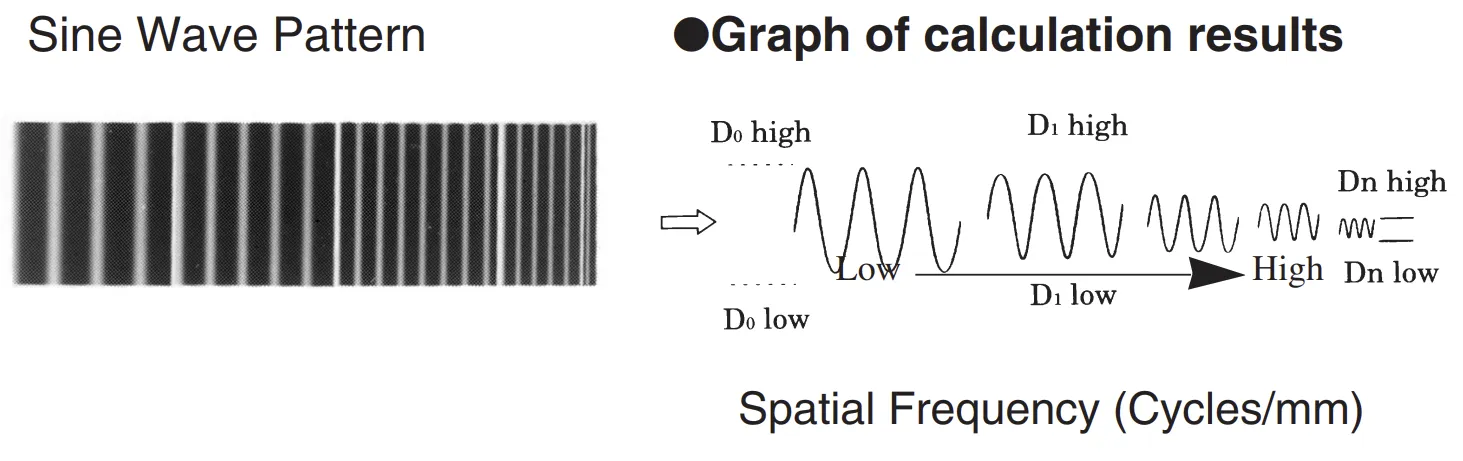
然后使用微密度计对不同空间频率的图案进行密度测量，得到上图中右侧所示的测量结果。

基于测得的密度值，在胶片特性曲线中找到对应的对数曝光值并求解出线性曝光值。

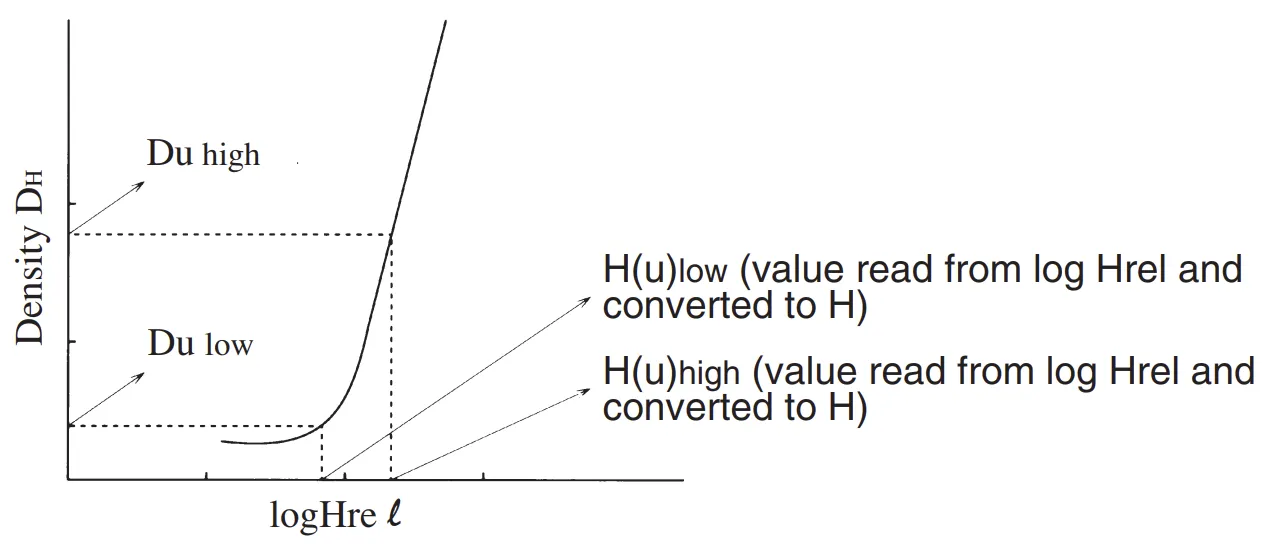
具体来说，方法如下：

• 测量光学密度：

使用密度计对图案的不同部分进行测量，得到其光学密度值。这些密度值是单位面积上入射光强与透过光强的比值的对数表示，通常表示为：

$$
D = \log_{10} \left( \frac{I_0}{I_t} \right)
$$
其中，$I_0$$是入射光强，$$I_t$是透过光强。

2.查找对数亮度值：

通过胶片或感光材料的特性曲线（通常为密度-对数曝光曲线），查找对应的对数亮度值。特性曲线给出了一定范围内的光学密度与特定曝光量（即对数亮度，通常用$\lg H$表示）之间的关系。

3.求解线性亮度值：

假设特性曲线给出的对数曝光值为 $\log_{10} H$，其中 $H$ 为线性曝光值。为了将对数曝光值转换为线性曝光值，需要进行指数运算，以便从对数曝光值 $\log_{10} H$ 求解出线性曝光值 $H$。

利用该空间频率下测得的最高曝光值$H(u){\mathrm{high}}$ 与最低曝光值 $H(u){\mathrm{low}}$ 可以计算该空间频率下的调制值 $M(u)$（亦可理解为当前空间频率下正弦函数的振幅）：

$$
M(u) = \frac{H(u){\mathrm{high}} - H(u){\mathrm{low}}}{H(u){\mathrm{high}} + H(u){\mathrm{low}}}
$$
再利用如下公式分别计算归一化每个空间频率下的$M(u)$（ $M(0)$ 代表空间频率为0时的调制值，即测试母版原生对比度 ），绘制得到MTF曲线。
$$
MTF(f) = 100%\times\frac{M(u)}{M(0)}
$$

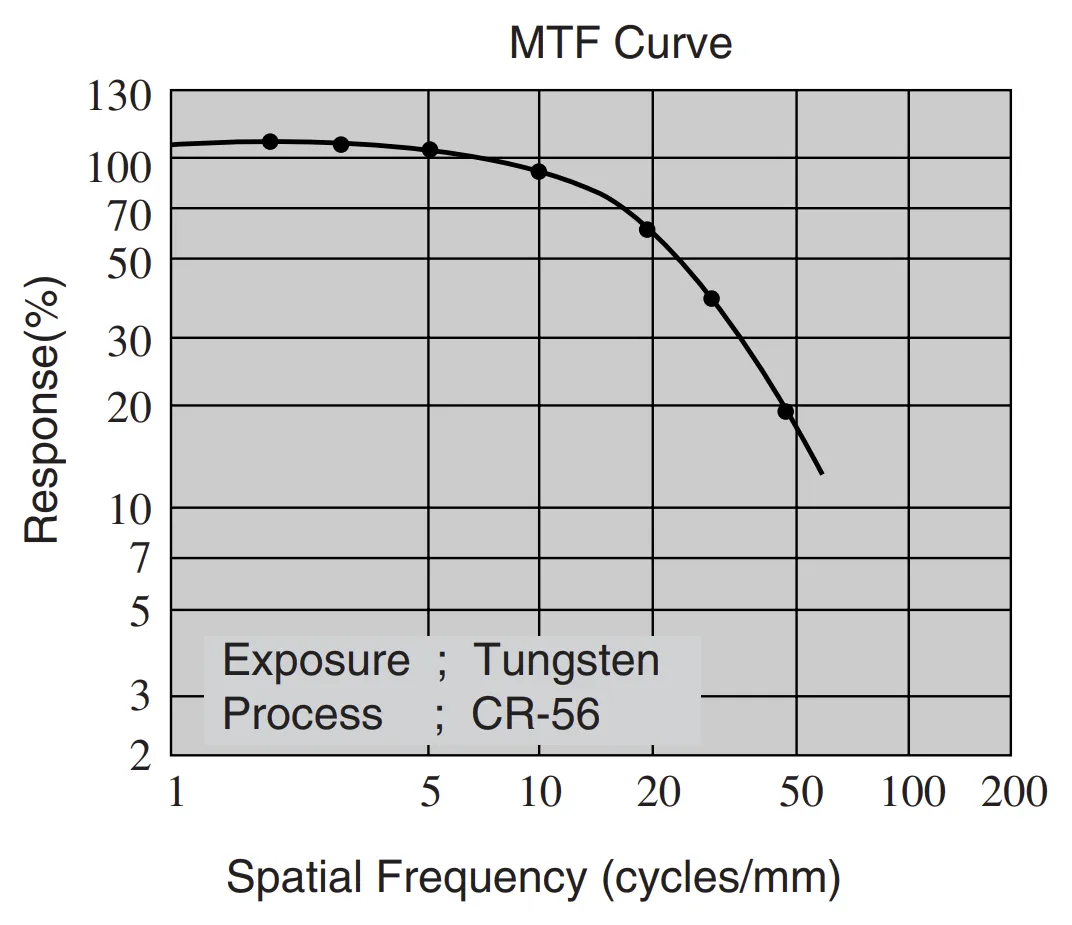
在MTF曲线图中，特定空间频率下的响应值越高，意味着图像还原得越好。同时还可以比较不同胶片的MTF曲线图来分析他们对不同频率细节的再现能力。

颗粒度

在将胶片负片放大显影在较大尺寸相片上时，胶片的颗粒结构会变得明显；而在普通尺寸的相片中这种情况并不明显。

虽然需要大约50倍的放大才能用肉眼看到感光乳剂中的单个晶体，但由于所谓的“团聚”现象，通常在较低的放大倍率下就能看到颗粒。“团聚”是由颗粒在乳剂中分布不均造成的现象。这在观看者的感知中产生了一种被称为“颗粒感”的感觉。

颗粒度通过一个心理物理技术获得的统计数值来表示，该统计数值反映了均匀曝光处理的感光材料区域中颗粒数量与大小分布的波动。

RMS颗粒度、Selwyn颗粒度、Q系数和其他方法被用来评估颗粒度。在这些方法中，RMS颗粒度由于其简单性以及与视觉颗粒感的良好对应关系而被广泛使用。

RMS的定义

RMS（Root Mean Square, 均方根）在统计学中用作标准偏差，表示一组测量值之间的差异，即偏差δ –（短横线代表偏差值的平均）的平方。因此，RMS越低，测得的密度值之间的差异（颗粒度）就越小。

测量方法

将待测的感光材料均匀曝光并进行处理。然后，用一个具备极小孔径开口（直径48µm）的微密度计扫描样本（样本的平均密度为1.0），通过计算银盐颗粒或染料云的微小密度变化的标准偏差值来确定RMS。作为一个平均值，密度值的分布大致符合正态分布。

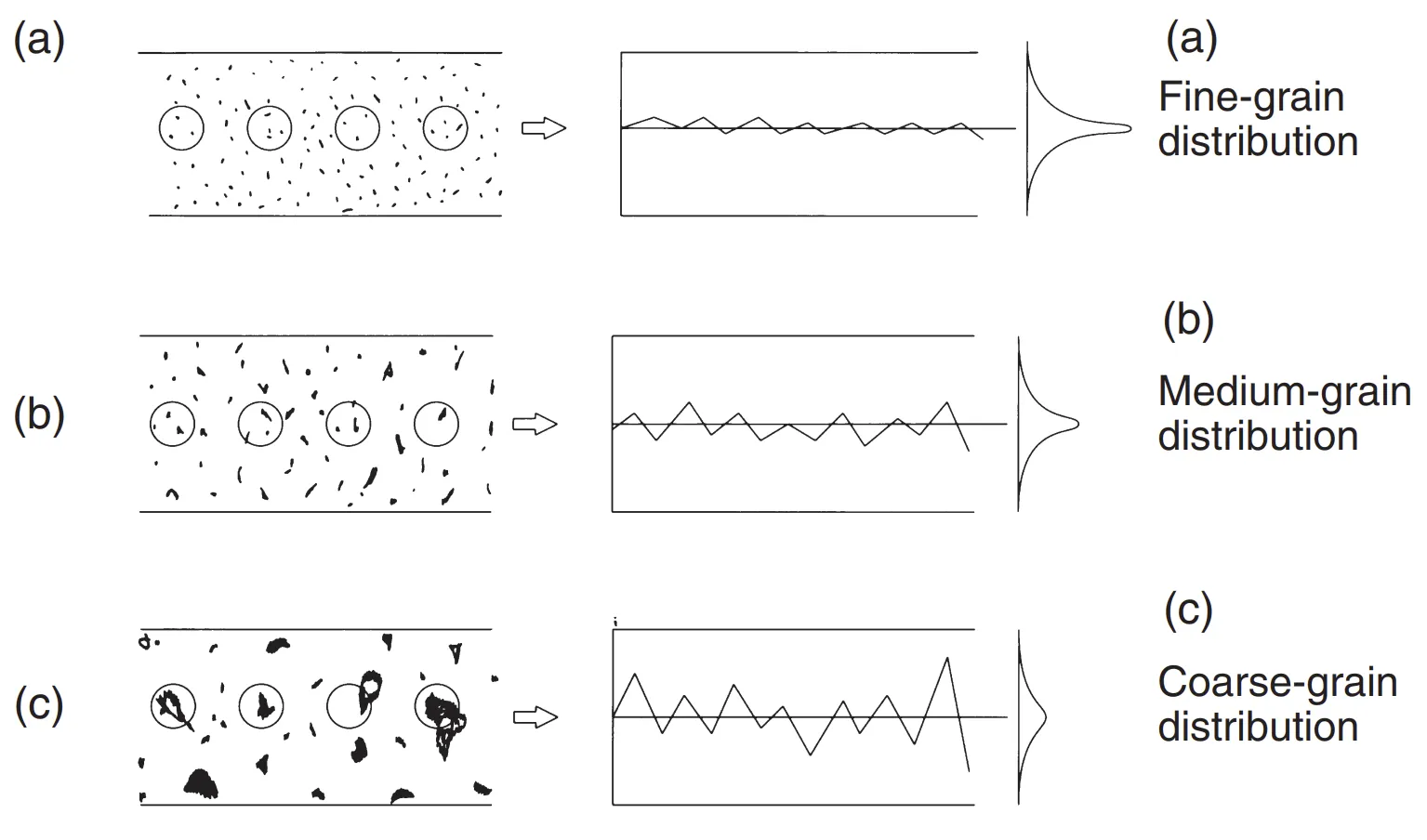
上图中左侧一列为卤化银颗粒或染料云在胶片中的分布；右侧一列为基于微密度计测量的密度变化和值分布；从上到下依次为：精细颗粒分布、中等颗粒分布与粗糙颗粒分布。

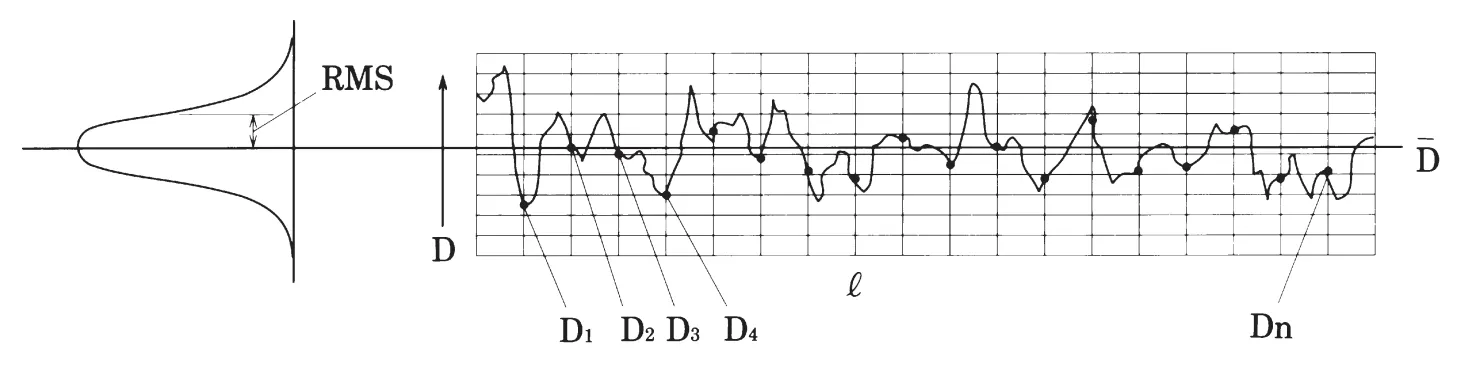
具体的RMS计算公式如下：
$$
RMS = \sqrt{ \frac{(D_1 - \overline{D})^2 + (D_2 - \overline{D})^2 + \cdots + (D_n - \overline{D})^2}{n - 1} }
$$

其中，$n$表示测定的密度值总数，$\overline{D}$表示测得的所有密度的平均值$
\overline{D} = \frac{\sum_{i=1}^{n} D_i}{n}
$,$D_{n}$代表每次测得的密度值。

动态范围

动态范围（Dynamic Range, DR）指相机可捕捉的光强的范围，通常表示为f-Stops或EV（曝光值）。通俗来讲，动态范围描述的是画面从具有影调细节的最暗的阴影部分，到最亮的高光部分的光强度分布范围。当拍摄的场景在亮度上有较大差异时，具有更大动态范围的胶片就能记录更多的影像细节。

胶片的动态范围可以通过分析H&D图像得到，在此之前，先让我们来理解一下H&D曲线。

H&D曲线与测量方法

感光材料的乳剂层经曝光和显影加工后，它的透明程度会由于金属银的淀积而降低。乳剂层透明度的降低与许多因素有关，在冲洗过程标准化的前提下，曝光量(H)就成了影响透明度最重要的因素。

为了寻找乳剂层透明程度与曝光量之间的数学关系，19世纪90年代英国两位学者——化学家H-Hurter和工程师V-Driffield用了约十年的时间，终于找到乳剂层中沉淀银的密度与曝光量及适当条件下的显影程度之间的比例关系，并建议用曝光量的对数和阻光率的对数（即密度）作为横纵坐标来表述它们之间的关系。这个坐标系后来被称为H-D曲线，也称为特性曲线，或者，曝光量-密度曲线。

横纵坐标都采用对数表示有着如下的特殊考量：

1.直观和一致的表示：

横坐标（对数曝光量，Log Exposure）：摄影胶片或者感光材料的动态范围通常很宽，曝光量可以在很大范围内变化。如果直接使用曝光量，曲线可能会在某些区域过于压缩，无法有效显示感光材料在不同曝光量下的响应。对数表示能够压缩宽广的曝光范围，使得不同曝光量下的效果更易于对比。

纵坐标（密度，Density）：密度是对数表示的阻光率。由于光线穿透材料时，强度往往呈指数下降，直接使用线性刻度会导致在低透射率（高密度）区域时数据难以区分，对数表示能够有效地体现从完全透光到完全不透光的宽广范围。

2.线性关系便于分析：

使用对数坐标能将非线性的响应关系转化为线性关系，这使得分析、比较和理解变得更加直观和简便。例如，在中间调区域，胶片密度与对数曝光量之间的关系往往呈现出近似线性。

3.符合人眼感知的对数特性：

人类的视觉感知本身具有对数特性。对数曝光和密度的表示方式更加接近人眼对光强和亮度变化的实际感知，更容易让人理解曝光变化对影像的影响。

4.技术标准化和一致性：

使用对数表示的方法已经在摄影、影像科学和各种技术应用中广泛接受和标准化。这样的标准化有助于保持方法和数据的一致性，并且使得不同胶片、曝光条件和处理方法下的结果可以方便地进行对比和交流。

由于曝光量通常用H表示，特性曲线的横标就是$\lg H$，所以H-D曲线实际是一语双关，既是指Hurter-Driffield曲线，也可以理解为曝光量(H)-密度(D)曲线。

实际上，特性曲线描述的就是胶片显影后不同曝光量与相应密度的关系。密度值来源于一系列胶片试条，这些试条经精确校正的感光计（Sensitometer）曝光，然后在严格标准下进行冲洗。每个试条上的照度（$E$，单位是勒克斯）乘以曝光时间（$t$，单位是秒）得到曝光量（$H$）：
$$
H = E \times t
$$

其单位是勒克斯-秒（lux-sec），也就是单位面积乳剂层上接受的光的总量。

用密度计测量每个试条上的透光率（Transmittance, T），即透过胶片的光通量$Q_{t}$与投射到材料上的光通量（入射光）$Q_{o}$之比，计算出阻光率（Opacity, O）。阻光率O等于透光率的倒数，即：

$$
O = \frac{1}{T} = \frac{Q_o}{Q_t}
$$
胶片依沉积银颗粒的多少，光线穿透率可以是100%、50%、25%、10%……0.01%，相对的透光率是 1.0、0.5、0.25、0.1……0.0001；相应地，阻光率是1、2、4、10……10,000。这样巨大的数字在制作曲线时很不方便，标尺过小会造成不够精确，故取阻光率O的以10为底的对数，称为密度(Density，D)，即：

$$
D = \lg O = \lg \left( \frac{Q_o}{Q_t} \right)
$$
上述数值对应的D就是0.0、0.3、0.6、1.0……4.0。

将H也取以10为底的对数（即$\lg H$）绘制横坐标，以密度(D)绘制纵坐标得到的曲线即为测试胶片的特性曲线。

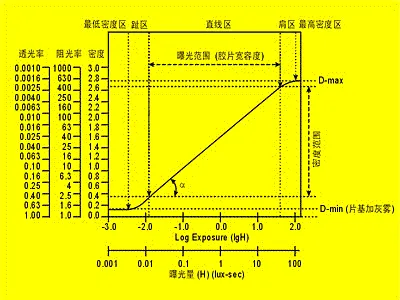
4.0一般是胶片所能达到的最高密度，所以纵坐标的最高值一般不大于4.0。横坐标上，曝光量每增加一倍，$\lg H$增加0.3单位。这可以简单地通过以下方式计算得出：

$$
\text{Log Exposure}{\mathrm{new}} = \log{10}(2 \cdot E) = \log_{10}(E) + \log_{10}(2)
$$

$$
\Delta \text{Log Exposure} = \log_{10}(2) \approx 0.3010
$$

从H&D曲线中读出动态范围

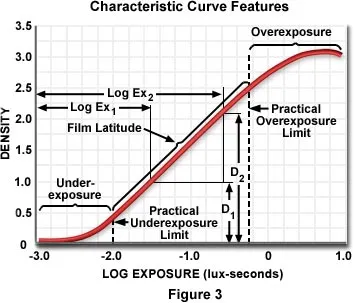
动态范围是由特性曲线的直线部分决定的。趾部、肩部虽然也能对光线作出一部分响应，并不是完全无响应或完全过曝，而且有些专业人士还非常擅长从趾部和肩部还原信息。但是，由于趾部和肩部存在严重的影调或细节失真，不能很好再现实际场景，因此作为一个普遍接受的概念，仍然只有胶片的直线响应区被认为是胶片的宽容度（上图中Film Latitude对应区域）。

例如，直线区横坐标跨越2.1单位，那么该胶片的宽容度是2.1/0.3 = 7，也就是该胶片有7档的宽容度。胶片的宽容度受到显影条件的影响，显影时间延长，平均梯度增大，宽容度要减小。

其他可从H&D曲线中读出的信息

H&D曲线除了包含胶片的动态范围信息外，还可以读出一些与图像成像质量并不直接相关，但在拍摄过程中不考虑就会获得不可用图像的指标。

• 感光度

感光度是胶片固有的对光反应的敏感性，是与在一定显影条件下产生的一定摄影效果的曝光量成反比的值。通俗地说，就是高感光度的胶片只需较少曝光量即能达到低感光度的胶片需较多曝光量所能达到的摄影效果。

感光度的测定是基于特性曲线计算出来的。以黑白片为例，美国标准协会(American Standard Association, ASA)是这样规定的：在求取特性曲线时，试条曝光后在指定的条件下进行精确控制显影，使得显影后获得的特性曲线满足以下条件——以曲线中灰雾+片基密度+0.1的密度为基准点，该基准点处的曝光量对数+1.3相对应的密度值应该等于0.8。如果符合这个条件，那么感光度S等于0.8除以基准点的曝光量。

例如，如果某黑白片的基准点曝光量是0.004lux/s，那么这款胶片的感光度就是0.8/0.004=200，如果是0.008lux/s，那么感光度就是100。

• 反差

指的是胶片中明暗色调的对比，通常所谓的胶片表现“平、软”或“层次鲜明、硬”实际就是在描述反差。

胶片的反差由特性曲线的斜率来体现。一般而言，曲线的斜率越陡峭，胶片的反差越高。常用Gamma值或平均梯度(Average Gradient)来量化反差。

Gamma就是特性曲线的直线区的斜率。Gamma不代表趾区和肩区的的反差，因此超出直线区的部分，如强高光部和暗部的反差不能用Gamma来描述。

平均梯度指的是特性曲线的两段连线的平均斜率，因此涵盖了趾区、直线区和肩区的影调。

胶片的Gamma值或平均梯度会因显影时间不同而改变，因此黑白负片一般会在Data Sheet里给出Time-Gamma曲线，可以根据这个曲线去对Gamma或平均梯度进行调控。但是，黑白反转片和所有彩色片的显影是标准化过程，无法用Gamma曲线去控制。

为了降低胶片的总体反差，可以在显影前对胶片用均匀光线进行闪光曝光，实际上就是提高胶片的灰雾密度，所以也称之为闪灰。