色彩科学Vol.5 色品图与普朗克轨迹

前言：从三维到二维

在《色彩科学Vol.4》中，我们建立了 CIE 1931 XYZ 色彩空间。虽然 XYZ 三刺激值完整地描述了颜色，但它是一个三维向量，不便于在平面媒介上展示和分析。

为了直观地描述颜色的“特性”（即色相和饱和度），我们需要将亮度信息剥离，只保留色度信息。这就引出了色品图的概念。此外，光源的颜色特性通常用色温来描述，这与物理学中的黑体辐射密切相关。

本章将绘制出色彩科学中最经典的“马蹄形”图案，并探讨普朗克轨迹与色温的数学定义。

CIE xy 色品坐标

为了将三维的 $(X, Y, Z)$ 投影到二维平面，我们定义归一化的色品坐标 $(x, y, z)$：

$$x = \frac{X}{X+Y+Z}, \quad y = \frac{Y}{X+Y+Z}, \quad z = \frac{Z}{X+Y+Z}$$

显然 $x+y+z=1$。因此，我们只需要 $(x, y)$ 两个坐标就可以唯一确定色度，而 $z$ 可以由 $1-x-y$ 导出。 结合亮度 $Y$，我们构成了 xyY 色彩空间。

CIE 1931 色品图

将可见光谱（380nm - 780nm）中所有单色光的 $(x, y)$ 坐标计算出来并连接，就形成了著名的光谱轨迹。

关键特征

• 马蹄形：光谱轨迹呈现倒 U 型或马蹄形。
• 光谱色：位于曲线边界上的点，代表饱和度最高的单色光。
• 紫线：连接 380nm（蓝紫端）和 780nm（红端）的直线。这条线上的颜色（品红、紫红）在光谱中不存在，只能由红光和蓝光混合而成。
• 等能白点：坐标 $(1/3, 1/3)$，代表光谱能量均匀分布的白色。

色域

根据格拉斯曼定律，任意两个颜色混合后的新颜色，必位于这两点连线之上。因此，由三个基色（如显示器的 R, G, B）构成的三角形区域，就是该设备能显示的全部颜色范围，称为色域。

普朗克轨迹

在色品图中，有一条贯穿白区的曲线格外重要，它描述了理想黑体在不同温度下的颜色变化，称为普朗克轨迹。

普朗克辐射定律

根据量子力学，绝对黑体（Blackbody）的光谱辐射出射度 $M_e(\lambda, T)$ 仅取决于其绝对温度 $T$（单位：开尔文 K）：

$$M_e(\lambda, T) = \frac{2\pi h c^2}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda k T}} - 1}$$

其中：

• $h$: 普朗克常数
• $c$: 光速
• $k$: 玻尔兹曼常数

轨迹的计算

对于给定的温度 $T$，我们可以计算出黑体辐射的光谱分布，进而计算其 XYZ 三刺激值和 xy 色品坐标：

$$X_T = \int M_e(\lambda, T) \bar{x}(\lambda) \mathrm{d}\lambda$$ $$x_T = \frac{X_T}{X_T + Y_T + Z_T}, \quad y_T = \frac{Y_T}{X_T + Y_T + Z_T}$$

随着温度 $T$ 从 $1000K$ 升高到 $\infty$，$(x_T, y_T)$ 在色品图上描绘出一条曲线，即普朗克轨迹。

• 低色温 (2000K-3000K)：偏红、黄（如烛光、白炽灯）。
• 中色温 (5000K-6500K)：接近纯白（如正午日光 D65）。
• 高色温 (8000K+)：偏蓝（如阴天天空）。

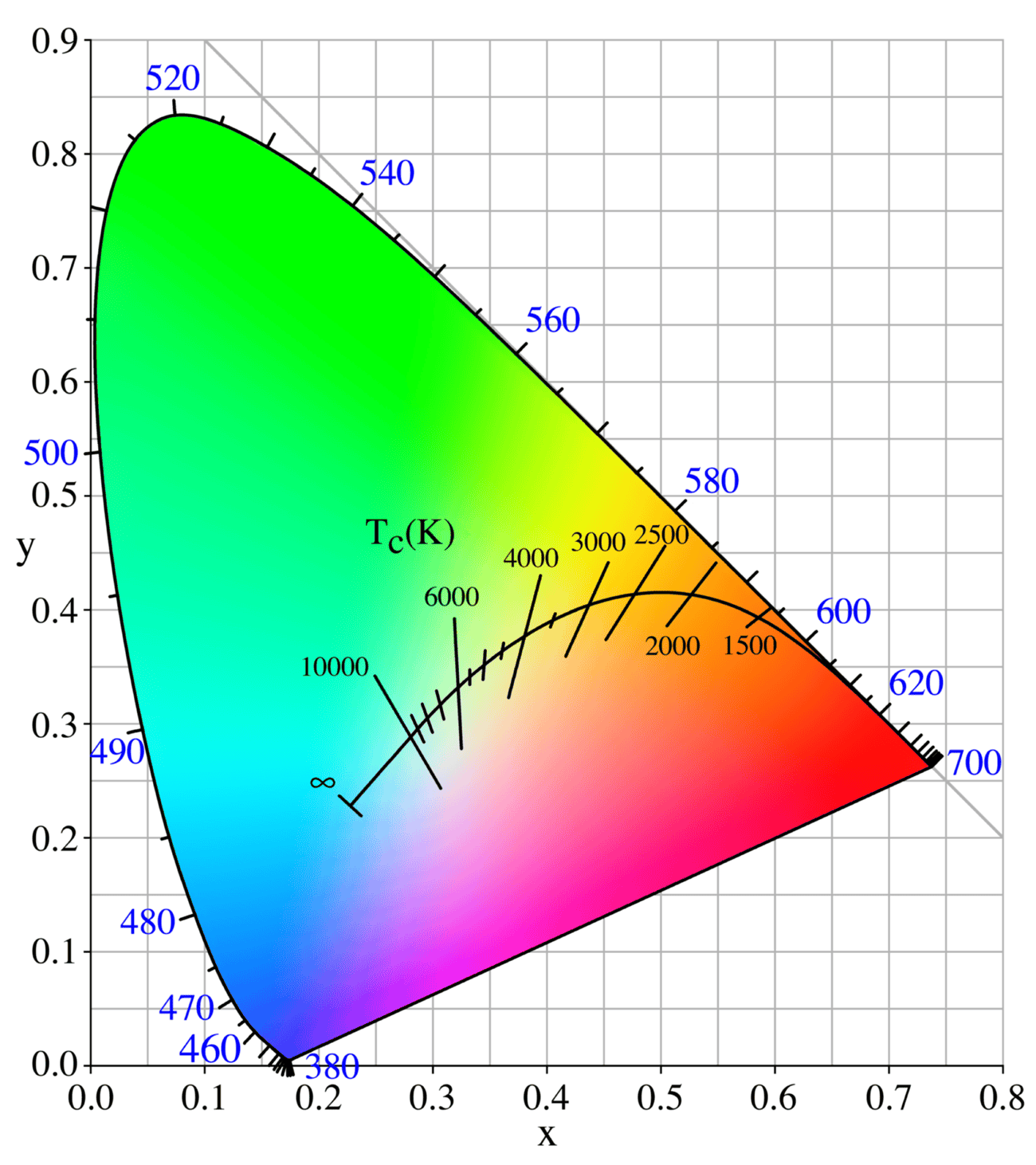
色温与相关色温

色温

如果一个光源的色品坐标正好落在普朗克轨迹上，我们称该黑体的温度为该光源的色温。

相关色温

大多数实际光源（如荧光灯、LED）的色品坐标并不完全在普朗克轨迹上。此时，我们寻找普朗克轨迹上距离该光源色品点最近的那个点的温度，称为相关色温。

为了定义“最近”，需要在 CIE 1960 UCS (Uniform Chromaticity Scale) 均匀色度图中计算欧氏距离，因为 CIE 1931 xy 图在视觉上是不均匀的。连接具有相同 CCT 点的线称为等温线。

总结与展望

CIE 1931 xy 色品图是色彩科学中最著名的图表，但它有一个致命的缺陷：视觉不均匀性。 在图中，绿色区域占据了巨大的面积，而蓝色区域却被压缩得很小。这意味着，在图中同样长度的距离，在绿色区域人眼几乎分辨不出差别，而在蓝色区域却代表着巨大的颜色差异。

为了解决这个问题，我们需要对色彩空间进行非线性变换，构建均匀色彩空间。这就是下一章《色彩科学Vol.6 均匀色彩空间：从Luv到Lab》的主题。

Reference

1. Planck, M. (1900). On the Theory of the Energy Distribution Law of the Normal Spectrum.
2. Wyszecki, G., & Stiles, W. S. Color Science: Concepts and Methods. Wiley.
3. McCamy, C. S. (1992). Correlated color temperature as an explicit function of chromaticity coordinates. Color Research & Application.